Read about our work recently published on Light: Science & Applications in a Special Issue on the “Topological photonics and beyond: novel concepts and recent advances”:

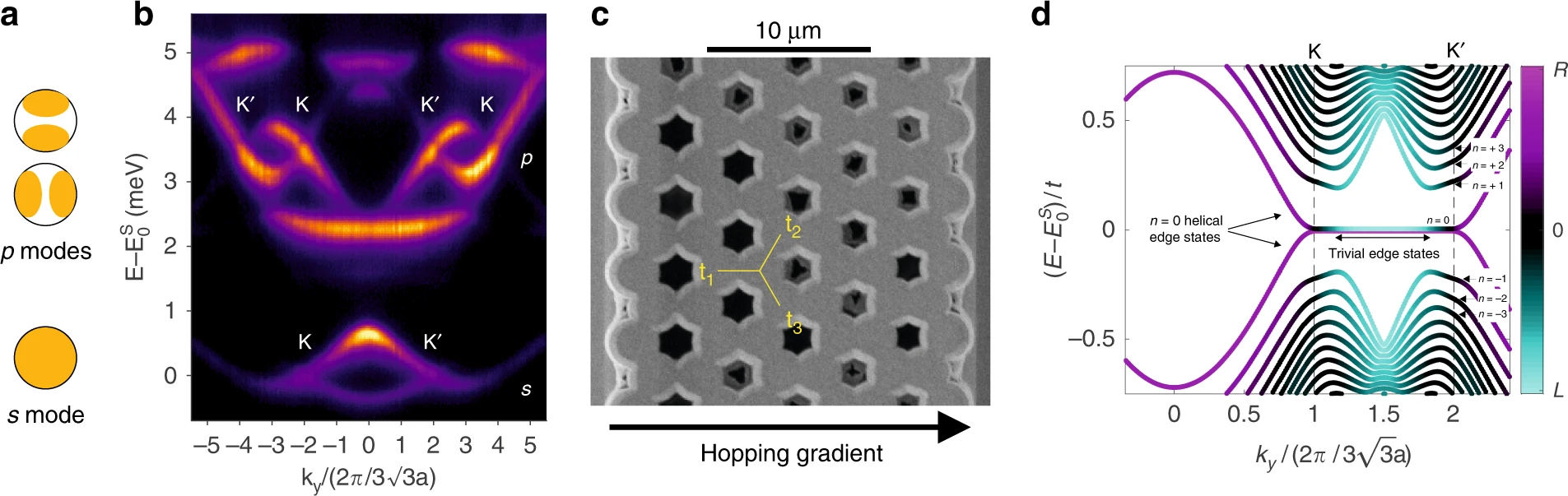
Direct observation of photonic Landau levels and helical edge states in strained honeycomb lattices

One among the many remarkable properties of graphene, a two-dimensional carbon allotrope, is that its low-energy excitations are described by a Dirac equation for massless fermions. An inhomogeneous strain introduced, for example, as an elastic deformation of the honeycomb lattice, is equivalent to an artificial pseudo-magnetic field: in this case the energy spectrum of the Dirac electrons shows the formation of relativistic Landau levels.

Artificial graphene materials, such as photonic honeycomb lattices, offer a tunable implementation of the strain through a spatial modulation of the tight-binding couplings or through a physical deformation of the lattice.

In our recent collaboration with the group of Alberto Amo and Jacqueline Bloch, we show a measurement of the lowest Landau level wavefunctions in a strained photonic honeycomb lattice, for which we provide direct evidence of the sublattice symmetry breaking, a distinctive feature of synthetic pseudo-magnetic fields. Our realization implements helical edge states associated with Landau levels, demonstrating experimentally a novel way of engineering propagating edge states in photonic lattices.

Click here to read more about our work. StrainedHoneycomb